441. Arranging Coins
Easy
You have n coins and you want to build a staircase with these coins. The staircase consists of k rows where the ith row has exactly i coins. The last row of the staircase may be incomplete.
Given the integer n, return the number of complete rows of the staircase you will build.
Example 1:
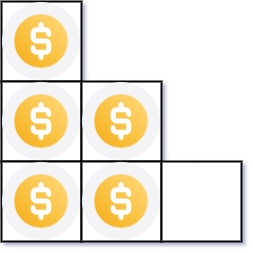
Input: n = 5
Output: 2
Explanation: Because the 3rd row is incomplete, we return 2.
Example 2:
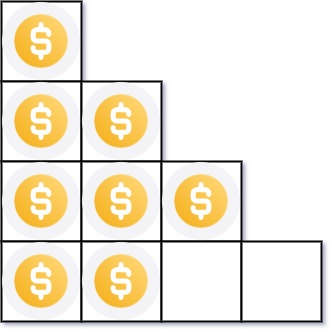
Input: n = 8
Output: 3
Explanation: Because the 4th row is incomplete, we return 3.
Constraints:
1 <= n <= 231 - 1
<내코드>
class Solution:
def arrangeCoins(self, n: int) -> int:
def ap(k):
return k * (k+1) // 2
if n == 1 :
return 1
low, high = 1, n
mid = 0
while low <= high :
mid = (low + high) // 2 # 1
print(mid)
ap_result = ap(mid)
print(ap_result)
if ap_result == n:
return mid
elif ap_result > n:
high = mid - 1
elif ap_result < n:
low = mid + 1
return high- 이분탐색으로 풀었는 문제임
- k * (k + 1) // 2 공식
=> 본 문제에서 계단량이 1,3,6 씩 증가하는것이 등차수열 합공식과 마찬가지라는것을 알게됨
이것으로 계단의 칸이 한칸씩 더 만들어질 때 마다 몇개의 동전이 필요한지 찾을 수 있음
- 이분탐색의 찾는 값 mid 값으로 계단에 총 동전 량을 찾음
=> 그런데 동전 량이 n 동전량보다 많은지 적은지에 따라 최적화된 값을 찾음
=> 최적화된 값은 최저동전량이 최대 동전량보다 커질 때 더이상 탐색할 수있는것이 없음
=> 이때 mid 가 최적화된 값
- mid 가 아니라 right 반환함
=> mid 반환하는 경우는 정확히 일치하기 때문에 mid 반환하는 것임
=> 하지만 right 반환 경우는 ap_result 가 n 을 초과하지 않는 최대값이기 때문
(문제의 요구사항이 최댓값 찾기)
<모범사례>
class Solution:
def arrangeCoins(self, n: int) -> int:
i=0
while n>=0:
i+=1
n=n-i
return i-1- 처음에는 다음 모범사례와 같이 n에서 i를 배가면서 n 이 음수가 될 때를 i를 리턴하는것을 생각함
=> 하지만 본 문제의 취지는 이분탐색이기 때문에 이용하지 않음
- 본 방식은 O(root n) 임
=> 이분탐색보다 비효율적임
<보충학습>
# 문제 1: 최소 제곱수 찾기
# 문제 설명:
# 정수 x가 주어졌을 때, x보다 크거나 같은 최소의 제곱수를 찾아 반환하세요.
# 예를 들어, x = 17인 경우, 17보다 크거나 같은 최소의 제곱수는 25 (5^2) 입니다.
#
# 입력:
# 정수 x (1 ≤ x ≤ 10^6)
# 출력:
# x보다 크거나 같은 최소의 제곱수
# 예시:
# 입력: 17
# 출력: 25
# 설명: 17보다 크거나 같은 최소의 제곱수는 25입니다.
def binary_square(x):
def square(num):
return num ** 2
low, high = 0, x
while low <= high:
mid = (low + high) // 2
square_num = square(mid)
if square_num == x:
return mid
elif square_num < x :
low = mid + 1
elif square_num > x :
high = mid - 1
return low**2
result = binary_square(17)
print(result)- 이번에는 '최소의 제곱수' 라는 최소와 관련된 것이기 때문에 low 를 이용함
'문제풀이 > 일일연습문제' 카테고리의 다른 글
| [DFS/BFS]99클럽 코테 스터디 30일차 TIL + 백준/Silver/6080. Bad Grass (0) | 2024.08.22 |
|---|---|
| [DFS/BFS]99클럽 코테 스터디 29일차 TIL + 백준/Silver/6188. Clear Cold Water (0) | 2024.08.21 |
| [Binary Search]99클럽 코테 스터디 27일차 TIL + 0268-missing-number (0) | 2024.08.19 |
| [stack/queue]99클럽 코테 스터디 26일차 TIL + 프로그래머스/2/42587. 프로세스 (0) | 2024.08.18 |
| [practice]99클럽 코테 스터디 25일차 TIL + 프로그래머스/1/172928. 공원 산책 (0) | 2024.08.17 |