933. Increasing Order Search Tree
Easy
Given the root of a binary search tree, rearrange the tree in in-order so that the leftmost node in the tree is now the root of the tree, and every node has no left child and only one right child.
Example 1:
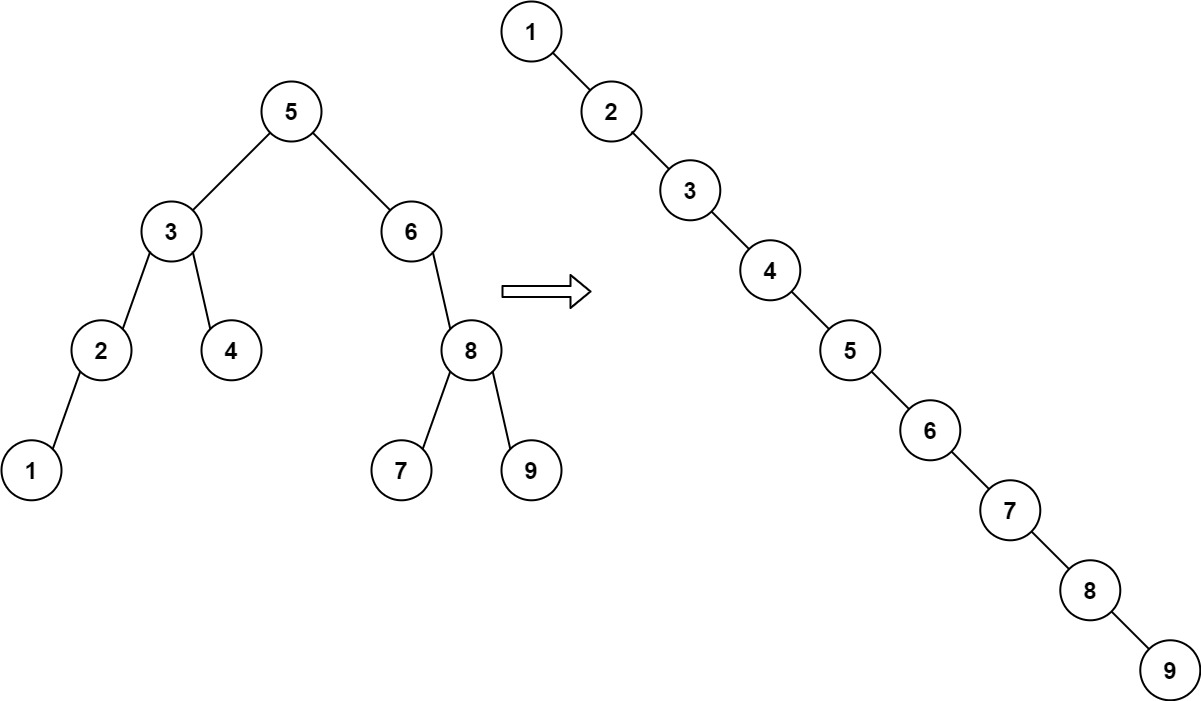
Input: root = [5,3,6,2,4,null,8,1,null,null,null,7,9]
Output: [1,null,2,null,3,null,4,null,5,null,6,null,7,null,8,null,9]
Example 2:
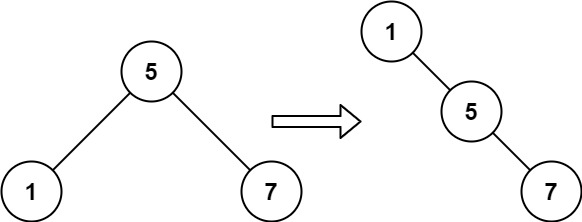
Input: root = [5,1,7]
Output: [1,null,5,null,7]
Constraints:
- The number of nodes in the given tree will be in the range
[1, 100]. 0 <= Node.val <= 1000
<내코드> : 2시간 경과
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def increasingBST(self, root: TreeNode) -> TreeNode:
def inorder_tree(root, list):
if root is not None:
inorder_tree(root.left, list)
# list.append(root.val) #node 값이 아니라 node 자체
list.append(root)
inorder_tree(root.right, list)
return list
nodes = inorder_tree(root,[])
# 새로운 트리의 더미 루트 노드 생성
dummy = TreeNode(0)
current = dummy
for node in nodes:
node.left = None # 왼쪽 자식 제거
current.right = node # 오른쪽 자식으로 설정
current = node # current를 갱신
return dummy.right
# list.sort(reverse = True) #리스트 정렬 생략
# print(list)
# 새로 생성 X
# new_root = TreeNode()
# new_root.val = list.pop()
# print(root)
# def right_tree(root: TreeNode, list) -> TreeNode:
# if root is None:
# return None
# # print(root)
# if root is not None:
# # print(root)
# # 왼쪽
# root.left = None
# # root 값
# root.val = list.pop()
# # 오른쪽
# # new_root = TreeNode()
# root.right = right_tree(root, list)
# return root
# print(root, list)
# return right_tree(root, list)- 일단 중위 순회 부분은 쉽게 바로 구현이 되었다. 나에게 익숙해져서 다행이다.
하지만..
- 다양한 방식에서 무엇이 바람직한건지 아직 좀 더 학습이 필요함
1. 헷갈린 부분
- 트리 재구성과 관련해서 지속적으로 값을 손대기가 어려
<모범사례>
class Solution:
def increasingBST(self, root: TreeNode) -> TreeNode:
vals = []
# Easy recursive Inorder Traversal to get our values to insert.
def inord(node):
if not node:
return
inord(node.left)
vals.append(node.val)
inord(node.right)
inord(root)
# Create a new tree to return.
tree = TreeNode(val=vals[0])
# Use a sentinel so we dont lose our tree location in memory.
tmp = tree
# Iterate through our vals, creating a new right node with the current val.
for i in vals[1:]:
tmp.right = TreeNode(val=i)
# Move the sentinel to the next node.
tmp = tmp.right
return tree- 나와 마찬기로 푼 방식
- vals 를 좀 더 큰 범위 변수로 두었음
- 값에 대한 list를 순회함 -> 순회하면서 트리의 오른쪽 node에 새로운 노드를 추가하고
추가한 노드를 다시 기본으로 하는 방식으로 순회함
<보충학습>
1. 실무에서의 트리 중위순회 활용
- 트리의 내용을 리스트로 만들거나, 트리의 구성을 재구성 하기
=> DB에서 중위 순회로 인덱스를 만들거나 정렬이 가능함
2. 추가 연습문제
- yield를 사용한 제너레이터 함수
이 부분을 사용해야할 필요성은 아직 모르겠음
'문제풀이 > 일일연습문제' 카테고리의 다른 글
| [DP]99클럽 코테 스터디 20일차 TIL + 0119-pascals-triangle-ii (0) | 2024.08.13 |
|---|---|
| [Greedy]99클럽 코테 스터디 19일차 TIL + 프로그래머스/1/135808. 과일 장수 (0) | 2024.08.09 |
| [DFS/BFS]99클럽 코테 스터디 17일차 TIL + 0094-binary-tree-inorder-traversal (0) | 2024.08.07 |
| [Brute Force]99클럽 코테 스터디 16일차 TIL + 프로그래머스/1/86491. 최소직사각형 (0) | 2024.08.07 |
| [Brute Force]99클럽 코테 스터디 15일차 TIL + 프로그래머스/1/42840. 모의고사 (0) | 2024.08.05 |