783. Search in a Binary Search Tree
Easy
You are given the root of a binary search tree (BST) and an integer val.
Find the node in the BST that the node's value equals val and return the subtree rooted with that node. If such a node does not exist, return null.
Example 1:
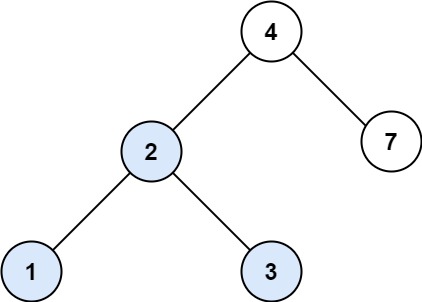
Input: root = [4,2,7,1,3], val = 2
Output: [2,1,3]
Example 2:
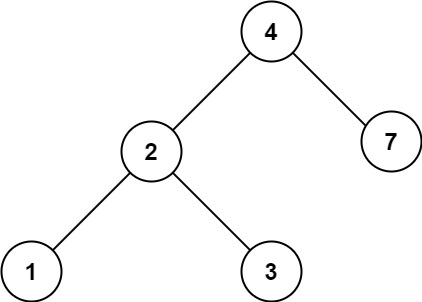
Input: root = [4,2,7,1,3], val = 5
Output: []
Constraints:
- The number of nodes in the tree is in the range
[1, 5000]. 1 <= Node.val <= 107rootis a binary search tree.1 <= val <= 107
----
총 소요시간 : 1H 40M
<내코드>
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def searchBST(self, root: Optional[TreeNode], val: int) -> Optional[TreeNode]:
if not root:
return None
if root.val == val:
return root
elif root.val < val:
return self.searchBST(root.right, val)
else:
return self.searchBST(root.left, val)
# def searchBST(self, root: Optional[TreeNode], val: int) -> Optional[TreeNode]:
# data = root
# while root is not None:
# if data == val:
# return self.subTree(root)
# elif data < val: #찾으려는 값이 더 크면 오른쪽으로
# return self.searchBST(root.right, val)
# elif data > val:
# return self.searchBST(root.left, val)
# return None
# def subTree(self, root : Optional[TreeNode]) -> Optional[TreeNode]:
# data = root.val
# subTree_list = TreeNode(data)
# if data is not None:
# subTree_list.left = TreeNode(root.left)
# subTree_list.right = TreeNode(root.right)
# return subTree_list
1. 헤맨부분
- 이진탐색트리에 대한 용도 (해시로도 충분히 탐색이 가능하지 않는가?)
=> BST가 O(h) [h == 높이] / 해시테이블이 O(1) 로서 해시테이블이 더 효율적이지만,
순서를 정해주는 경우 BST가 더 용이하다.
정리하면 세트, 딕셔너리의 key가 정렬된 상태가 필요하다면 연산의 효율성이 다소 낮아짐에도 불구하고 BST가 필요하다.
- 반복문과 재귀를 이중으로 사용해버림
=>
# def searchBST(self, root: Optional[TreeNode], val: int) -> Optional[TreeNode]:
# data = root
# while root is not None:
# if data == val:
# return self.subTree(root)
# elif data < val: #찾으려는 값이 더 크면 오른쪽으로
# return self.searchBST(root.right, val)
# elif data > val:
# return self.searchBST(root.left, val)
# return Nonewhile을 빼던가, 재귀를 빼던가 둘 중 하나를 했어야했음
특히 정답코드의 조건문 간에 모두가 return 이 있는 이유는 한쪽으로 조건이 갈라지면 더이상 그쪽으로 갈 일이 전혀 없고 점점 깊이를 더해가야하기 때문임
즉 순회가 아니라 탐색이기 때문임
- root 라는 인자 자체가 return 이 되어서 subtree가 될 수있는가?
=> root 자체가 재귀를 하면서 sub tree가 충분히 될 수 있음
왜냐하면 처음부터 들어오는 인자타입이 그러하기 때문임
<모범사례>
from typing import Optional
# Definition for a binary tree node.
class TreeNode:
def __init__(self, val=0, left=None, right=None):
self.val = val
self.left = left
self.right = right
class Solution:
def searchBST(self, root: Optional[TreeNode], val: int) -> Optional[TreeNode]:
if not root:
return None
if root.val == val:
return root
elif root.val < val:
return self.searchBST(root.right, val)
else:
return self.searchBST(root.left, val)
# Example usage
# Constructing the tree [4,2,7,1,3]
root = TreeNode(4)
root.left = TreeNode(2)
root.right = TreeNode(7)
root.left.left = TreeNode(1)
root.left.right = TreeNode(3)
solution = Solution()
result = solution.searchBST(root, 2)
# The result will be the subtree rooted at the node with value 2<보충학습>
1. BST 학습
삽입 : 저장하기 위한 위치를 찾아가는 것 (기존 값과 비교하여 left, right 를 비교하면서 찾아감)
-> 이 경우 삽입되어야하는 위치에 값이 있는경우 그 값을 다른곳으로 이동시켜야함
탐색(검색) : 마찬가지로 비교하면서 찾아감
삭제 : leaf 인지 여부에 따라 달리 판단이됨 (추후 학습)
'문제풀이 > 일일연습문제' 카테고리의 다른 글
| [Brute Force]99클럽 코테 스터디 15일차 TIL + 프로그래머스/1/42840. 모의고사 (0) | 2024.08.05 |
|---|---|
| [BST*]99클럽 코테 스터디 14일차 TIL + 0101-symmetric-tree (1) | 2024.08.04 |
| [sort]99클럽 코테 스터디 12일차 TIL + 프로그래머스/1/12917. 문자열 내림차순으로 배치하기 (0) | 2024.08.02 |
| [sort]99클럽 코테 스터디 11일차 TIL + 프로그래머스/1/12933. 정수 내림차순으로 배치하기 (0) | 2024.08.01 |
| [heap]99클럽 코테 스터디 10일차 TIL + 0789-kth-largest-element-in-a-stream (0) | 2024.07.31 |